Monty Hall Problem Simulator

ਮੌਂਟੀ ਹਾਲ ਦੀ ਸਮੱਸਿਆ ਸੰਭਾਵੀ ਥਿਊਰੀ ਦੇ ਖੇਤਰ ਵਿਚ ਸਭ ਤੋਂ ਮਸ਼ਹੂਰ ਗਣਿਤਕ ਸਮੱਸਿਆਵਾਂ ਵਿਚੋਂ ਇਕ ਹੈ:

ਇੱਕ ਟੈਲੀਵਿਜ਼ਨ ਗੇਮ ਵਿੱਚ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ਹੋਸਟ ਨੇ ਇੱਕ ਖਿਡਾਰੀ ਨੂੰ ਖਿਡਾਰੀਆਂ ਦੇ ਸਾਹਮਣੇ ਤਿੰਨ ਬੰਦ ਦਰਵਾਜ਼ਿਆਂ ਵਿੱਚੋਂ ਇੱਕ ਚੁਣਨ ਲਈ ਕਿਹਾ ਹੈ. ਦੋ ਦਰਵਾਜ਼ੇ ਦੇ ਪਿੱਛੇ ਬੱਕਰੀਆਂ ਹਨ ਅਤੇ ਇਕ ਦਰਵਾਜ਼ੇ ਦੇ ਪਿੱਛੇ ਇਕ ਕਾਰ ਹੈ ਜਿਸ ਨੂੰ ਖਿਡਾਰੀ ਉਸ ਦਰਵਾਜ਼ੇ 'ਤੇ ਚੜ੍ਹ ਕੇ ਜਿੱਤ ਸਕਦਾ ਹੈ. ਖਿਡਾਰੀ ਨੇ ਇਕ ਦਰਵਾਜਾ ਚੁਣਿਆ ਹੈ (ਜੋ ਬੰਦ ਹੈ), ਹੋਸਟ ਨੇ ਇਕ ਹੋਰ ਦਰਵਾਜੇ ਖੋਲ੍ਹਿਆ ਜਿਸਦੇ ਪਿੱਛੇ ਇਕ ਬੱਕਰੀ ਹੈ. ਹੋਸਟ ਫਿਰ ਖਿਡਾਰੀ ਨੂੰ ਪੁੱਛਦਾ ਹੈ ਕਿ ਕੀ ਉਹ ਉਸ ਦਰਵਾਜ਼ੇ 'ਤੇ ਰਹਿਣਾ ਚਾਹੁੰਦਾ ਹੈ ਜੋ ਉਹ ਸ਼ੁਰੂ ਵਿਚ ਚੁਣਿਆ ਸੀ ਜਾਂ ਕੀ ਉਹ ਦੂਜੇ ਬੰਦ ਦਰਵਾਜ਼ੇ' ਤੇ ਜਾਣਾ ਚਾਹੁੰਦਾ ਹੈ.

ਸਵਾਲ ਇਹ ਸਪਸ਼ਟ ਹੈ ਕਿ ਕੀ ਖਿਡਾਰੀ ਦਰਵਾਜ਼ੇ 'ਤੇ ਸਵਿਚ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਜਾਂ ਚੁਣੇ ਹੋਏ ਦਰਵਾਜ਼ੇ' ਤੇ ਰਹੇ?

ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਕਹਿ ਸਕਦੇ ਹਨ ਕਿ ਇਸ ਨਾਲ ਕੋਈ ਫ਼ਰਕ ਨਹੀਂ ਪੈਂਦਾ ਕਿ ਖਿਡਾਰੀ ਦਰਵਾਜ਼ੇ 'ਤੇ ਚੜ੍ਹਦਾ ਹੈ ਜਾਂ ਨਹੀਂ, ਕਿਉਂਕਿ ਕਾਰ ਨੂੰ ਜਿੱਤਣ ਦੀ ਸੰਭਾਵਨਾ 50/50 ਹੈ, ਹਾਲਾਂਕਿ ਇਹ ਸਹੀ ਜਾਪਦਾ ਹੈ, ਕਿਉਂਕਿ ਦੋ ਇੱਕੋ ਜਿਹੇ ਬੰਦ ਦਰਵਾਜ਼ੇ ਹਨ, ਇਹ ਗਲਤ ਜਵਾਬ ਹੈ.

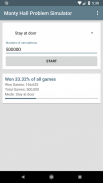
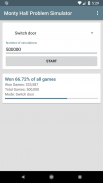
ਸਹੀ ਉੱਤਰ ਇਹ ਹੈ ਕਿ ਕਾਰ ਜਿੱਤਣ ਦਾ ਮੌਕਾ 67% ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਖਿਡਾਰੀ ਦਰਵਾਜ਼ੇ 'ਤੇ ਸਵਿਚ ਕਰਦਾ ਹੈ ਅਤੇ ਸਿਰਫ 33% ਜਦੋਂ ਖਿਡਾਰੀ ਦਰਵਾਜ਼ੇ' ਤੇ ਰਹਿੰਦਾ ਹੈ ਤਾਂ ਉਹ ਪਹਿਲਾਂ ਚੁਣਿਆ ਗਿਆ ਸੀ.

ਵਿਸ਼ਵਾਸ ਨਾ ਕਰੋ ਅਜੇ ਮਿਲੇ ਹੋਏ ਹਨ? ਬਸ ਐਪ ਨੂੰ ਡਾਊਨਲੋਡ ਕਰੋ ਅਤੇ ਇਸਨੂੰ ਆਊਟ ਕਰੋ!

ਇਹ ਐਪ ਤੁਹਾਨੂੰ ਇੱਕ ਲਾਈਨ ਵਿੱਚ 5 ਮਿਲੀਅਨ ਤੱਕ ਦਾ ਵਰਣਿਤ ਗੇਮ ਦ੍ਰਿਸ਼ ਨੂੰ ਆਟੋਮੈਟਿਕਲੀ ਰੂਪ ਦੇਣ ਲਈ ਆਗਿਆ ਦਿੰਦਾ ਹੈ. ਤੁਸੀਂ ਇਹ ਚੋਣ ਕਰ ਸਕਦੇ ਹੋ ਕਿ ਕੀ ਤੁਸੀਂ ਸਿਮੂਲੇਟਡ ਖਿਡਾਰੀ ਨੂੰ ਹਮੇਸ਼ਾ ਦਰਵਾਜ਼ਾ ਬਦਲਣਾ ਚਾਹੁੰਦੇ ਹੋ ਜਾਂ ਹਮੇਸ਼ਾਂ ਦਰਵਾਜੇ ' ਐਪ ਦੁਆਰਾ ਖੇਡਾਂ ਦੀ ਮੰਗ ਕੀਤੀ ਗਈ ਗਿਣਤੀ ਨੂੰ ਸਿਮਟ ਕੀਤੇ ਜਾਣ ਤੋਂ ਬਾਅਦ, ਇਹ ਤੁਹਾਨੂੰ ਇੱਕ ਅੰਕੜੇ ਮੁਹੱਈਆ ਕਰਦਾ ਹੈ ਜੋ ਤੁਹਾਨੂੰ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ਪਲੇਅਰ ਕਿੰਨੀਆਂ ਖੇਡਾਂ ਜਿੱਤੀਆਂ ਹਨ. ਇਸ ਤਰੀਕੇ ਨਾਲ ਤੁਸੀਂ ਇਹ ਦੱਸ ਸਕਦੇ ਹੋ ਕਿ ਕੀ ਖਿਡਾਰੀ ਨੂੰ ਦਰਵਾਜ਼ੇ ਨੂੰ ਨਹੀਂ ਬਦਲਣਾ ਚਾਹੀਦਾ ਜਾਂ ਨਹੀਂ.